
Обработка материала по изменчивости методами математической статистики
Современное учение об изменчивости является научной областью, которая пользуется очень широко приемами математической статистики, а поэтому нам неизбежно придется познакомиться с этими приемами, без знания которых невозможно понять современное учение о «породах» медоносной пчелы.
Предположим, нами просчитано число зацепок на левом заднем крыле у 100 экземпляров рабочих пчел данного улья. Получены такие цифры: 21, 20, 18, 19, 24, 22 и так далее. Можно подсчитать, сколько же раз попались пчелы с числом зацепок 18, сколько с 19 зацепками и т. д. Сделав это для всех 100 пчел, получим следующий, так называемый вариационный ряд:
| Число зацепок в крыле | 18 19 20 21 22 23 24 25 |
| Число пчел с данным числом зацепок | 2 5 10 22 24 17 12 8 |
Видно, что пчел с 18 зацепками была две, с 19 — пять и т. д.
Вариационный ряд можно изобразить графически. На горизонтальной оси помечено число зацепок, а над соответственным числом зацепок в виде вертикальной черты изображено приходящееся сюда число случаев. Если соединить вершины вертикальных линий друг с другом, то получится ломаная линия, которая носит название вариационной кривой (см. рис. 8).
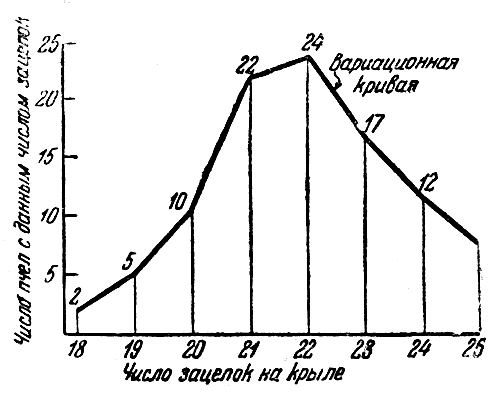
Рис. 8. Вариационная кривая числа зацепок на заднем крыле рабочих пчел (Алпатов, 1927)
Первой и основной характеристикой вариационного ряда является среднее арифметическое. Чтобы его получить, надо сложить все 100 чисел, характеризующих зацепки крыльев вышеприведенной семьи пчел — +21 +20 +18 и т. д., и сумму разделить на 100. Если наш материал уже классифицирован в вариационный ряд, для быстроты можно заменить сложение умножением каждой цифры, показывающей число случаев, на стояющую над ней величину. Все эти произведения надо просуммировать и разделить на 100.
Среднее арифметическое условно принято обозначать буквой М.
В нашем примере вычисление дает следующее:
М = (2,18 + 5,19 + 10,20 + 22,21 + 24,22 + 17,23 + 12,24 + 8,25)/100=22,00
Кроме вопроса о среднем арифметическом ряде, его типе, ибо свойство М таково, что оно является центром, вокруг которого налево и направо распределяется одинаковое количество отдельных случаев (При так называемом «нормальном» распределении ), может возникнуть вопрос, насколько сильно рассеиваются вокруг типа отдельные случаи. Раньше для учета этого явления пользовались указанием размеров самого мелкого и самого крупного экземпляра вариационного ряда. В нашем примере указали бы границы 18—25.
Теперь же по ряду соображений принято пользоваться так называемым стандартным отклонением и коэфициентом изменчивости или вариации.
Получаются эти величины так. Возьмем в нашем примере пчел с 18 зацепками. Каждая отклоняется от М на 4 зацепки. Квадрат четырех 16. Так как таких пчел две, то для них имеем 16х2=32.
Хотя отклонение было с отрицательным знаком, но вследствие возведения в квадрат отрицательные знаки уничтожаются. Для пчел с 19 зацепками имеем 3х3х5 = 45. Суммируя все таким образом найденные произведения, деля сумму на число всех случаев — 100, получаем среднее квадратическое уклонение, а извлекши из него квадратный корень, получаем стандартное отклонение (стандарт по-английски — тип), обозначаемое греческой буквой σ (сигма). Для нашего примера имеем:
σ = ± √ (16,2 + 9,5 + 4,10 + 1,22 + 1,17 + 4,12 + 9,8)/100 = ± √2,76 = ± 1,661 зацепок.
Сигма — величина именованная и выражается в тех же единицах как изучаемый признак. Геометрический смысл сигмы таков. Если взять много материала (например 1000 пчел) и по вышеизложенному начертить вариационную кривую, то она будет весьма плавно подниматься и перегибаться над М. Если отложить налево и направо от М по отсеку, равному сигме, то место перехода каждой ветви кривой из вогнутой в выпуклую будет как раз приходиться над наружными точками сигм (см. рис. 9).
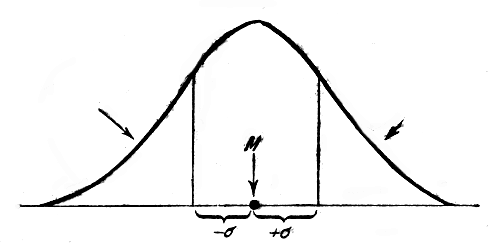
Рис. 9. Схема, поясняющая положение перелома ветвей нормальной кривой над точками, лежащими на расстоянии одной сигмы от среднего арифметического (Алпатов, 1927)
Ясно, что чем больше сигма, тем дальше будут эти точки находиться от М, тем уплощеннее будет кривая, тем больше будет рассеянность отдельных особей вокруг типа.
Для возможности сравнивать изменчивость признаков, выражаемых разными единицами измерений и дающих ряды с различной величиной М, придумали характеристику отвлеченную. Ее находят, выражая сигму ряда в процентах среднего арифметического данного ряда по формуле
С% = (σ•100)/М = (1,661•100)/22 = 7,54%.
Это — коэфициент вариации или коэфициент изменчивости.
Так вычисляют средние арифметические и стандартные отклонения для признаков счетных (число зацепок, число яйцевых трубочек и т. д.). Несколько иначе поступают, когда приходится иметь дело с признаками, получаемыми путем измерений, взвешиваний и т. д. При этом признаки особей пчел или целых семей выражаются не целыми числами, а числами с дробями (например 25,1 кг меда с семьи и т. д.). В этом случае при составлении вариационного ряда: и вариационной кривой составляют шкалу классов и разносят по классам измерения особей или семей. Возьмем в качестве примера определения, времени остановки движения 15 особей пчел, помещенных в атмосферу паров серного эфира. Цифры в минутах и долях минуты таковы: 6,25; 8,5; 5,0; 8,0; 6,25; 6,5; 3,5;, 6,5; 4,25; 4,4; 4,8; 7,8; 5,25; 5,75 и 6,7. Сперва надо наметить пределы вариации: 3,5 до 8,5 минут. Предположим, что мы хотим создать классы величиной в 2 минуты. Toгда шкала классов будет такова: 3—5—7—9. Всего у нас будет три класса. Для того чтобы на границу класса не попал ни один случай, припишем к каждой границе 0,01. Границы будут обозначаться; 3,01—5,01—7,01—9,01, а весь вариационный ряд после распределения показателей всех 15 пчел будет таков:
| Шкала классов | 3,01 - 5,01 - 7,01 - 9,01 |
| Число пчел в классе | 5 7 3 |
Вычисление среднего арифметического и стандартного отклонения можно вести как для вариационных рядов счетных признаков (см. выше пример с зацепками), только надо принимать, что частоты — число пчел в классе — относятся как бы к середине класса, например пять пчел в первом классе падают на 4,01 минуты, 7 —на 6,01.
В биометрических сочинениях приведенная нами характеристика типа — среднее арифметическое — и характеристики разбросанности отклонений вокруг типа — стандартное отклонение и коэфициент вариации, сопровождаются так называемыми средними и вероятными ошибками. Значение этих ошибок в биометрии необычайно велико. Дело в том, что когда мы определяем среднее число зацепок у ста пчел одной семьи, нас не интересуют именно эти 100 пчел, а интересует среднее число зацепок на крыльях всех пчел этой семьи, из которой в качестве пробной группы взято 100 штук. Оказывается, что о действительной средней величине нашего признака можно сделать заключение на основе пробы, причем характеристики, носящие название средних и вероятных ошибок, дают нам возможность сделать это заключение с такой точностью и уверенностью, с какой мы это пожелаем. Здесь не место выводить применяемые формулы; укажем, что формула для средней ошибки среднего арифметического такова: m = σ/√N , а для вероятной — РЕ= 6,6745(σ/√N) (m есть сокращенное условное обозначение средней ошибки, а РЕ — вероятной), где N — число случаев пробы.
Для нашего примера с зацепками
m = 1,661/√100 = 1,661/10 = 0,17
Теория вероятности отрасль математики, которая лежит в основе математической статистики, учит, что если к среднему арифметическому прибавить тройную среднюю ошибку: 22,0 + 3х0,17 = 22,51 и вычесть ее из него 22—3х0,17 = 21,49, то мы получаем такие пределы: 21,49 — 22,51. В этих пределах с уверенностью, которую практически можно считать достоверностью (998 шансов против 2 в пользу нашего утверждения), лежит среднее арифметическое всего материала, из которого мы взяли пробу и который нас собственно и интересует. Если пользоваться вероятной ошибкой, т. е. величиной, равной приблизительно семи десятым средней ошибки (множитель 0,6745), то для получения той же степени достоверности надо брать не утроенную среднюю ошибку, а вероятную ошибку, помноженную на 4,5. Наконец, ошибки имеют большое применение, когда нам надо сравнить две характеристики двух пробных групп и сделать заключение о том, отличаются ли средние тех исходных групп, из которых мы взяли пробу. Предположим, у нас промерены пробы пчел из Москвы и Харькова в отношений длины их хоботка. Первые дали среднюю длину в 6,115±0,003 мм, а вторые 6,549±0,003 мм. Насколько достоверны эти отличия? Находят разницу 6,549 — 6,115 = 0,434 и ее вероятную ошибку по следующей формуле:
РЕ=± PE12+PE22
которая гласит, что вероятная ошибка разницы средних равна корню квадратному из суммы квадратов ошибок сравниваемых средних. Если разница превышает свою ошибку в 4, 5 или больше раз, мы вправе говорить о статистической достоверности различия всех харьковских и московских пчел. В нашем примере это так и есть, ибо 0,434 в 108 раз больше, чем
РЕ = ± √0,0032+0,0032 = 0,004.
В этой книге всюду вычислены вероятные ошибки.
Желающие познакомиться более подробно с приемами математико-статистического материала, должны обратиться к специальным учебникам и пособиям. До сих пор сохранило свое значение пособие Ю. А. Филипченко «Изменчивость и методы ее изучения», 4-е издание. Очень полезна книга Митропольского: «Техника статистического исчисления»; крайне полезна для биологов и агрономов краткая, но очень доступная книжка нашего виднейшего математика-статистика В. Романовского (1947).
Для лиц, которым придется производить много вычислений, я не могу не рекомендовать технику вычисления, разработанную мною в итоге многолетней работы по биометрии и очень сильно облегчающую счетную работу (Алпатов, 1935).
Очень большое ускорение работы дает также пользование логарифмической линейкой.

|
ПОИСК:
|
© GEOMAN.RU, 2001-2020
При использовании материалов сайта активная ссылка обязательна:
http://animal.geoman.ru/ 'Мир животных'
При использовании материалов сайта активная ссылка обязательна:
http://animal.geoman.ru/ 'Мир животных'